Last news...

Publication of Introduction aux vibrations aleatoires by Dunod

Random mechanics, especially the study of random vibrations, is an important field in engineering. The applications are numerous in transportation, aeronautic, aerospace but also energy industries. This book is up-to-date synthesis of a course given in Ecole centrale de Lyon, France at the master level. It gathers in a coherent way all the material required in structural vibration, signal processing, and probability theory. This book aims to provides students, researchers, and engineers with all keys to investigate this fundamental science of engineering.

Available here

A. Le Bot, Introduction aux vibrations aleatoires, Dunod, 2018.

Publication of Foundation of statistical energy analysis in vibroacoustics by Oxford University Press

This book provides an in-depth study of the foundations of statistical energy analysis, with a focus on examining the statistical theory of sound and vibration. In the modal approach, an introduction to random vibration with application to complex systems having a large number of modes is provided. For the wave approach, the phenomena of propagation, group speed, and energy transport are extensively discussed. Particular emphasis is given to the emergence of the diffuse field, the central concept of the theory. All important notions are gradually introduced---making the text self-contained---to lead the reader to the ultimate result of `coupling power proportionality' and the concept of `vibrational temperature'. Further key topics include the analogy between thermodynamics and sound vibration. Applications are concerned with random vibration in mass--spring resonators, strings, beams, rods, and plates but also reverberation in room acoustics, radiation of sound, and sound response.

Available here

A. Le Bot, Foundation of statistical energy analysis in vibroacoustics, Oxford University Press, may 2015.

The squeal noise of a rubber-glass contact is controlled by Stribeck's law

The origin of the squeal of wiper blades or other rubber joints rubbing against glass surfaces is less obvious than it eppears at first sight. We have performed an experiment to explore systematically the domain of squealing and observed that it appears during the transition between the boundary and hydrodynamic regimes. But the origin of the transition remains mysterious...

The ripples in water are induced by the rubber glass instability.

F. Deleau, D. Mazuyer, A. Koenen, Sliding friction at elastomer/glass contact: Influence of the wetting conditions and instability analysis, Tribology International, vol. 42, 2009.

J. Le Rouzic, A. Le Bot, J. Perret-Liaudet, M. Guibert, A. Rusanov, L. Douminge, F. Bretagnol, D. Mazuyer, Friction-induced vibration by Stribeck’s law: application to wiper blade squeal noise, Tribology Letters, vol. 49, p. 563-572, 2013.

The noise induced by the rubbing of rough surfaces is not proportional to the contact area!

We realized an experiment to check if the friction noise of sliding rough surfaces is proportional to the contact area. We found that no! This result is not intuitive. A naive reasoning would state that the more numerous are the sliding solids, the higher is the noise they emit. Read more...

Experiment to measure the friction noise versus contact area.

A. Le Bot and E. Bou Chakra, Measurement of friction noise versus contact area of rough surfaces weakly loaded, Tribology Letters, vol. 37, p. 273-281, 2010.

A. Le Bot, E. Bou Chakra and G. Michon Dissipation of vibration in rough contact, Tribology Letters, vol. 41, p. 47-53, 2011.

V.H. Dang, J. Perret-Liaudet, J. Scheibert, A. Le Bot, Direct numerical simulation of the dynamics of sliding rough surfaces, Computational mechanics, vol. 52, pages 1169-1183, 2013.

The concept of entropy in statistical vibroacoustics

Up to now, statistical vibroacoustics and its main theory, statistical energy analysis, is entirely based on the application of energy balance. But if the analogy with thermodynamics is often underlined, it is never said what happens with the concept of entropy. We have discussed the second principle of thermodynamics in the framework of statistical energy analysis and introduced the concept of “vibrational entropy” and the “vibrational temperature” of sub-systems In steady-state condition, we have shown that the entropy exchanged with exterior by sources and dissipation exactly balances the production of entropy by irreversible processes at interface between sub-systems. Read more...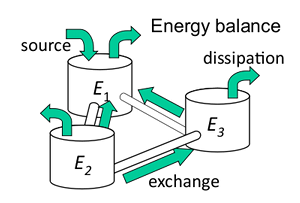

Statistical energy analysis for complex structures. Sub-systems behave like tanks for vibrational energy but also vibrational entropy. The first principle states the exchanges of vibrational energy between sus-systems and the second principle the exchanges of vibrational entropy.

A. Le Bot, Entropy in statistical energy analysis, Journal of the Acoustical Society of America, vol. 125, p. 1473-1478 , 2009.

A. Le Bot, A. Carcaterra, D. Mazuyer, Statistical vibroacoustics and entropy concept, Entropy, vol. 12, p. 2418-2435, 2010.

Statistical energy analysis is not a high frequency method!

It is usually claimed that statistical energy analysis is a high frequency theory of vibroacoustics. To check this assertion, we have applied the dimensional analysis to rectangular plates and have identified four dimensionless numbers for the validity of SEA: The mode count N, the modal overlap M, the normalized attenuation factor m and the coupling strength. Numerical experiments performed by solving the governing equations by the 'brute force' confirm that the validity domain of SEA in the frequency-damping loss factor plane is a narrow strip which upper limit dreceases with frequency. An increase of frequency with a constant damping loss factor may lead to get out the validity domain! Read more...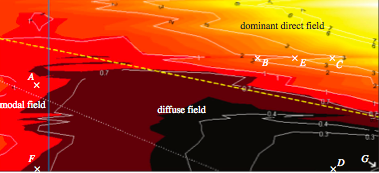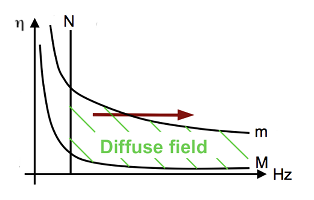

Left, Validity domain of SEA in the frequency-damping plane (dark zone). Right, At high frequency SEA no longer applies.

A. Le Bot and V. Cotoni, Validity diagrams of statistical energy analysis, Journal of Sound and Vibration, vol. 329, p. 221-235, 2010.

T. Lafont, N. Totaro, A. Le Bot, Review of statistical energy analysis hypotheses in vibroacoustics, Proceedings of the Royal Society A, In Press, 2014.