





 |
 |
 |
  |
 |
High frequency in vibroacoustics.Classical methods in acoustics and structural dynamics are based on the resolution of the governing equation by finite element method. But the latter requires a fixed number of degrees of freedom per wavelength. And since the more the frequency increases, the more the wavelength decreases, the total number of degrees of freedom rapidly becomes huge. 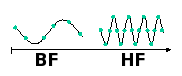
In high frequencies the wavelength is small and the number of degrees of freedom is largeDue to limited capabilities of computers, finite element softwares cannot perform calculations up to the high frequency range.
Maximal frequency by finite element method for a model of the order of million degrees of freedom.The increase of frequency also induces an increase of the number of natural modes of structure. Rapidly, the population of modes becomes very large. Thus, the mathematical methods based on the development of solution on modal basis become intractable. Numerical models require the knowledge of many parameters such as exact geometry, material properties, applied forces... But some of them are generally not well-known and we must consider that all input data have an uncertainty. However, results of computation become more sensitive to uncertainty when the frequency increases. So, even if we had very strong computers capable of doing calculations up to infinite frequency, those results would be not reliable. 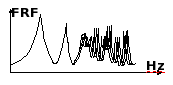
In high frequencies, the sensitivity is large. Frequency response functions of different calculations do not match.The principles of SEA.SEA is a recent theory of vibroacoustics [1, 2]. This is a theory well suited to complex structures vibrating in the high frequency domain. It is based on the application of concepts and methods of statistical physics to the study of energy exchange between acoustical and mechanical components. The pioners of SEA were largely inspired by statistical physics and recent advances in SEA continue to be inspired by it. SEA is a demonstration that in engineering sciences, conceptual revolution is still possible. Modes are the sites where energy is localized. They play a crucial role in SEA. Their number is assumed to be large (large population) and no mode plays a particular role (no dominant individual behaviour). Vibrating and acoustical sources are random. Then, the repartition of vibrational energy over modes is in perpetual modification. Modes are grouped to constitute sub-systems. A sub-system is defined as a packet of similar modes in which energy is equally shared. They can be structural components like rod, beam, plate, shell, acoustical cavity but, they can be also a mode packet within a structural component like flexural modes in plate or longitudinal modes or torsional modes in rods. The most important assumption defining sub-systems is the equipartition of energy. Whithin all sub-systems, vibrational energy is shared between modes. Equipartition means that the time-averaged energy is the same for all modes of a sub-system. A structure is thus divided in n sub-systems. This decomposition is macroscopic in the sense that all sub-systems must contain much modes. Sub-systems must therefore not be too small. Typically, a complex structure can be divided in a couple of dozen or hundreds sub-systems at most. 
Complex structures are splitted in structural or acoustical components called sub-systems.Sub-systems behave like tanks containing various forms of energy, acoustical or vibrational, longitudinal, transverse, flexural waves... These tanks can receive, can dissipate but also can exchange energy with their neighbours. The common features to these different kinds of energy are that they are all localized in the same frequency bandwidth 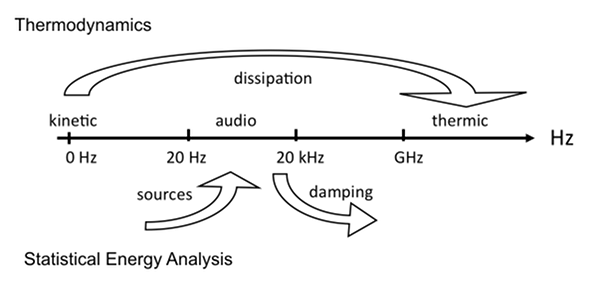
SEA focuses on energy transfers of audio frequency band while thermodynamics applies to thermal frequencies.Energy and SEA.All sub-systems can receive vibrational energy supplied by random sources, can dissipate energy and can exchange energy with neighbour sub-systems. In steady-state regime, the energy balance of sub-system i reads, 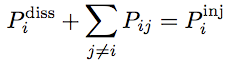 (1) (1)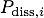 is the dissipated power, is the dissipated power, 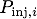 is the power being injected by sources and is the power being injected by sources and 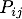 is the net power exchanged with sub-system j. is the net power exchanged with sub-system j.
The power dissipated in sub-system i is proportional to its vibrational energy
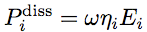 (2) (2)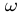 is the central circular frequency (rad/s) of the octave band. is the central circular frequency (rad/s) of the octave band.
Other energy exchanges are taken into account in a similar manner than internal dissipation. Thus, the energy lost by sub-system i towards sub-system j reads, 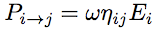 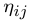 is called coupling loss factor. This equation is similar to previous one for internal dissipation. It must also be considered that sub-system j can provide sub-system i with, is called coupling loss factor. This equation is similar to previous one for internal dissipation. It must also be considered that sub-system j can provide sub-system i with,
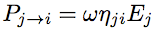 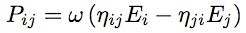 (3) (3)Coupling loss factors 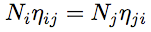 (4) (4)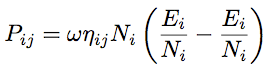 (5) (5)By substituting equations (2) and (5) into the power balance (1), one obtains a set of linear equations on the unknowns 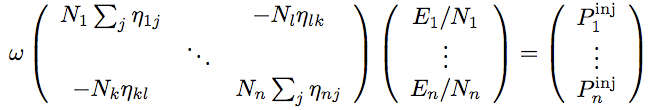 (6) (6)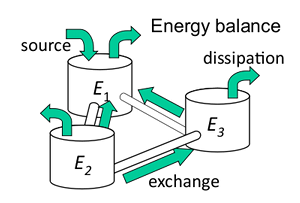
Energy exchanges in SEA. Sub-systems behave like energy tanks. All tanks can receive, disspate or exchange energy.Entropy and SEA.A SEA sub-system is a packet of N resonators whith increasing natural frequencies. Its vibrational energy is E. But since sources are random, the repartition of this energy over the N modes is fluctuating. The only mean energy E is supposed to be known.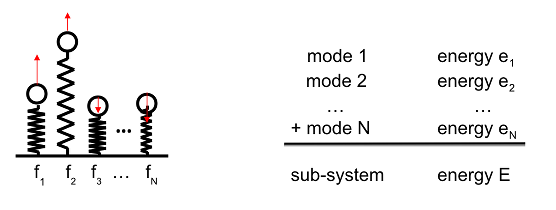
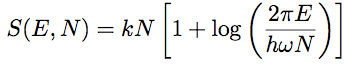 (6) (6)
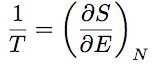
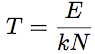 (7) (7)
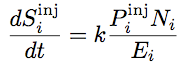
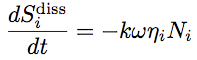
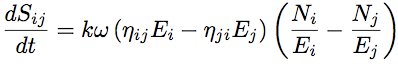
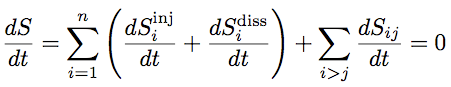

Vibroacoustical entropy exchanges in SEA. All sub-systems behave like entropy tanks.These tanks can receive, dissipate and create entropy by mixing energy.Validity of SEA.Four parameters are required to define the validity domain of SEA [3, 5]
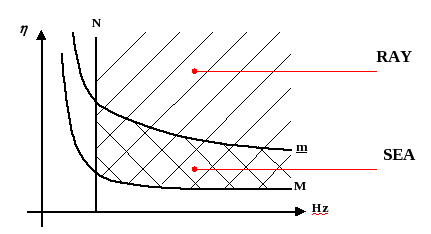
Validity domain of SEA for flexural vibration of a single plate.In the frequency - damping space, these four parameters limit the validity domain of SEA. The line N=cte is vertical, the lines m=cte and M=cte are hyperbolas. The validity domain of SEA is a strip extending up to high frequencies. The ray method only requires the two conditions N>>1 and M>>1 without the two other conditions so that the validity domain of rays is larger than those of SEA. A recent theory.
Some applications.All fields of mechanical industry are concerned, aerospace, automotive, railway, energy, weapon... SEA is a powerful tool for design and optimization of structures. It allows to know energy fluxes and therefore to elaborate efficient solutions to stop the flowing of vibrational energy. Nowadays, SEA has been adopted by almost all industries. SEA has been attractive to designers mainly because of its original insight into structural dynamics more than the efficiency of its predictive results. Towards non-equilibrium thermodynamics…The main difficulty encountered when applying SEA is the generally too low number of degrees of freedom in usual systems of order of few hundreds modes to be compared with Avogadro's number Bibliography.[1] R.H. Lyon, Statistical Energy Analysis of Dynamical Systems: Theory and Application, Cambridge, Massachusetts, MIT Press, 1975. [2] R.H. Lyon and R.G. DeJong, Theory and Application of Statistical Energy Analysis, Boston, Butterworth-Heinemann, 1995. [3] A. Le Bot, Derivation of statistical energy analysis from radiative exchanges, Journal of Sound and Vibration, vol. 300, p. 763-779, 2007. [4] A. Le Bot, Entropy in statistical energy analysis, Journal of the Acoustical Society of America, vol. 125, p. 1473-1478 , 2009. [5] A. Le Bot and V. Cotoni, Validity diagrams of statistical energy analysis, Journal of Sound and Vibration, vol. 329, p. 221-235, 2010. [6] A. Le Bot, A. Carcaterra, D. Mazuyer, Statistical vibroacoustics and entropy concept, Entropy, vol. 12, p. 2418-2435, 2010. |