Vibroacoustique

La vibroacoustique est l'étude des vibrations structurales, de l'acoustique et de l'interaction entre les vibrations et le son. Les phénomènes sont riches et variés. Il est toutefois d'usage de les classer de la manière suivante,

1 La propagation vibratoire et acoustique,

2 La réflexion, la diffraction et l'absorption des ondes aux frontières,

3 La transmission du son au travers les structures,

4 Le rayonnement acoustique des structures,

5 La réponse structurale à une excitation acoustique.

Voici un exemple de mise en équation d'un problème de vibroacoustique. Le problème est en dimension deux. On considère une structure (plaque) dont la déformée transverse à tout instant est v(x,t), en interaction avec un milieu fluide où se propage un champ de pression acoustique p(x,y,t). Le repère est précisé par la figure ci-dessous.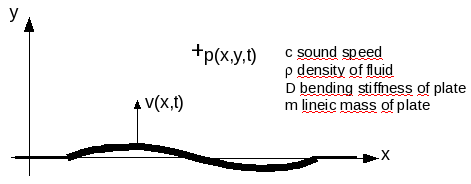

Exemple de problème vibroacoustique en deux dimensions. Le fluide est présent dans le domaine y>0 et la structure est en y=0.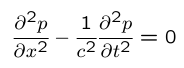

La déformée transverse v(x,t) de la structure suit l'équation de Love adaptée à la dynamique d'une plaque mince en vibration de flexion,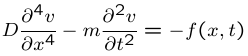

Enfin, les conditions de couplage entre le milieu fluide (acoustique) et la structure (plaque de Love) traduisent la continuité des vitesses à la surface de la structure,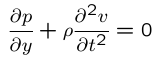

On doit y adjoindre des conditions aux limites pour le fluide ainsi que pour la structure mais aussi des conditions initiales (fluide et structure) permettant de fermer mathématiquement le problème. L'ensemble des équations (1), (2) et (3), conditions aux limites et initiales forme un problème vibroacoustique.

Tous les phénomènes de la vibroacoustique sont contenus dans ce système d'équations aux dérivées partielles. La résolution de ce système par voie analytique n'est possible que dans quelques rares cas. Elles donnent lieu à des calculs très techniques reposant souvent sur un usage intensif de l'analyse complexe.

Les trois bandes de fréquences.

Pour chaque problème vibroacoustique, on peut définir trois zones fréquentielles. Les basses, les moyennes et les hautes fréquences.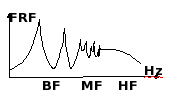

Les trois zones fréquentielles sont : les basses fréquences (BF) les modes sont peu nombreux et bien séparés, les moyennes fréquences (MF) une zone intermédiaire, les hautes fréquences (HF), les modes sont nombreux et indiscernables.

Il existe plusieurs manières de définir les domaines fréquentielles. En voici une adaptée à la discussion menée sur ce site.

1 Les fréquences sont basses lorsque la longueur d'onde de la vibration ou la longueur d'onde acoustique est plus grande ou du même ordre de grandeur que la taille du système considéré.

2 Les moyennes fréquences forment une zone intermédiaire.

3 Les hautes fréquences sont le domaine où la longueur d'onde est petite devant la taille du système.

On observe que la notion de basses ou hautes fréquences dépend de la taille du système (les hautes fréquences commencent à quelques kilohertz une petite salon et à quelques centaines de hertz pour un auditorium). Elles dépendent aussi de la structure du système (une structure souple est plus rapidement à hautes fréquences qu'une structure raide).

Les méthodes numériques habituellement employées pour résoudre les équations différentielles d'un couplage vibroacoustique sont les suivantes :

1 La méthode des éléments finis. C'est la méthode la plus répandue. Elle est bien adaptée au systèmes finis tels que des structures ou des salle fermées.

2 La méthode des éléments de frontière. C'est une méthode moins répandue mais qui est mieux adaptée dans le cas des systèmes non bornés comme le rayonnement en champ libre.

3 Méthode mixte, élément finis pour la structure bornée et éléments de frontière pour la partie acoustique.

4 Tir de rayon. C'est une méthode répandue en acoustique des salles pour résoudre des problèmes à hautes fréquences sous l'hypothèse de l'acoustique géométrique.