





 |
 |
 |
  |
 |
Les hautes fréquences en vibroacoustique.Les méthodes classiques de calcul des structures soumises à des vibrations reposent sur la résolution des équations du mouvement par la méthode des éléments finis. Celle-ci requiert de mailler la structure avec un nombre fixe d’éléments par longueur d’onde. Or, à mesure que la fréquence augmente, la longueur d’onde diminue et le nombre de degrés de liberté total devient rapidement considérable. 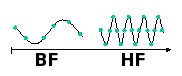
A hautes fréquences la longueur d’onde est petite et le nombre de degrés de liberté total est grandEn raison des capacités limitées des calculateurs, les codes éléments finis ne permettent pas de réaliser des calculs vibroacoustiques jusqu'à des fréquences très élevées.
Fréquences maximales accessibles par calculs éléments finis pour un modèle de l'ordre du million de degrés de liberté.L'augmentation du nombre de degrés de liberté s'accompagne d'une augmentation du nombre de modes propres de la structure. A hautes fréquences, la population de modes devient très importante. Les modèles numériques nécessitent la donnée exacte de la géométrie, des caractéristiques des matériaux, des excitations... Mais celles-ci ne sont connues qu'avec une certaine incertitude. Or les résultats du calcul sont d'autant plus sensibles aux incertitudes que la fréquence est élevée. On se retrouve donc dans la situation suivante. Même si nous disposons de la puissance de calcul suffisante pour réaliser les calculs à haute fréquence, ceux-ci ne sont pas fiables. 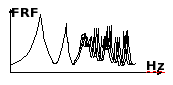
A haute fréquence, la sensibilité est importante. Les fonctions de réponse en fréquence pour différents calculs ne se superposent pas.Les principes de la SEA.La SEA est une théorie récente de la vibroacoustique [1, 2]. C'est une théorie adaptée aux systèmes complexes dans le domaine des hautes fréquences. Elle repose sur l'application des concepts et méthodes de la physique statistique à l'étude des échanges d'énergie vibratoire et acoustique entre les structures mécaniques. Les pionniers de la SEA se sont d'ailleurs largement appuyés sur la physique statistique et les développements récents de la SEA continuent de s'en inspirer. La SEA est la preuve que les sciences pour l’ingénieur connaissent encore des révolutions conceptuelles. Les modes sont les sites portant l'énergie vibratoire. Ils sont supposés nombreux (grande population) et ordinaires (pas de comportement individuel dominant). Les sources vibratoires et acoustiques sont aléatoires. Ainsi, la répartition de l'énergie vibratoire sur les modes est en perpétuelle modification. Les modes sont groupés pour former les sous-systèmes. Un sous-système est donc défini comme un ensemble de modes de même nature échangeant rapidement de l'énergie. Il peut s'agir d'un élément structural, une poutre, une plaque, une cavité acoustique mais il peut aussi s'agir d'un paquet de modes d'un élément structural, comme les modes de flexion d'une plaque ou les modes longitudinaux ou transverses. Une hypothèse importante permettant de définir les sous-systèmes est que l'équipartition modale de l'énergie doit être vérifiée. Cela signifie que dans chaque sous-système, les modes recoivent en moyenne la même énergie délivrée par les sources. Une structure complexe est ainsi divisée en n sous-systèmes. Cette décomposition est macroscopique en ce sens que chaque sous-système doit contenir un nombre suffisant de modes. Les sous-sytèmes ne doivent donc pas être trop petits. Typiquement, une structure très complexe pourra être divisée en quelques dizaines ou centaines de sous-systèmes tout au plus. 
Les structures complexes sont divisées en éléments structuraux ou acoustiques appelés sous-systèmes.Les sous-systèmes constituent des réservoirs d’énergie de différentes natures, acoustique ou vibratoire, ondes longitudinales, transverses, de flexion… Ces réservoirs peuvent recevoir de l’énergie, en dissipent mais aussi en échangent avec les réservoirs voisins. Le trait commun à ces différentes énergies est qu'elles sont toutes situées dans la même bande de fréquences 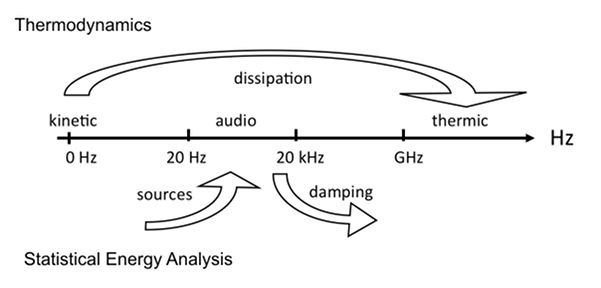
La SEA étudie les transferts d'énergie de la gamme audio tandis que la thermodynamique décrit les transferts de la gamme thermique.Energie et SEA.Chaque sous-système peut recevoir de l'énergie vibratoire fournie par les forces excitatrices ou les sources sonores, dissiper une part de cette énergie et échanger de l'énergie avec les sous-systèmes voisins. En régime permanent, le bilan énergétique du sous-système i s'écrit, 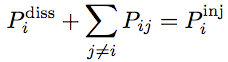 (1) (1) est la puissance dissipée, est la puissance dissipée, 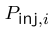 est
la puissance délivrée par les sources et est
la puissance délivrée par les sources et 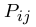 est la puissance échangée avec le sous-système j voisin. est la puissance échangée avec le sous-système j voisin.
La puissance dissipée dans le sous-système i est proportionnelle à l'énergie vibratoire
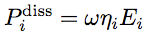 (2) (2)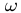 est la pulsation (rad/s) centrale de la bande d'octave étudiée. est la pulsation (rad/s) centrale de la bande d'octave étudiée.
Les échanges d'énergie avec les sous-systèmes voisins sont traités de la même manière que les pertes d'énergie. Ainsi l'énergie perdue par le sous-système i vers le sous-système j s'écrit, 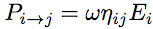 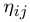 est appelé facteur de perte par couplage. Cette équation est tout-à fait semblable à l'équation précédente de perte par dissipation. Il faut aussi considérer que le sous-système j fournit de l'énergie au sous-système i, est appelé facteur de perte par couplage. Cette équation est tout-à fait semblable à l'équation précédente de perte par dissipation. Il faut aussi considérer que le sous-système j fournit de l'énergie au sous-système i,
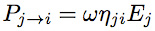 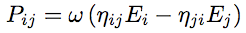 (3) (3)Les facteurs de perte par couplage 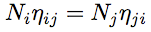 (4) (4)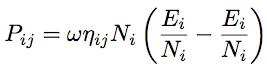 (5) (5)En substituant les équations (2) et (5) dans le bilan de puissance (1), on obtient un
système d'équations linéaires sur les inconnues 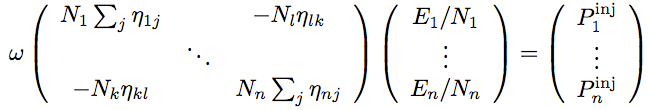 (6) (6)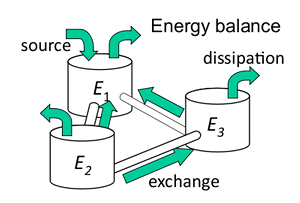
Echanges d’énergie vibroacoustique en SEA. Les sous-systèmes se comportent comme des réservoirs d'énergie. Chaque réservoir peut recevoir, dissiper et échanger de l’énergie.Entropie et SEA.Un sous-système SEA est un paquet de résonateurs harmoniques dont les fréquences propres, au nombre de N, sont croissantes. Son énergie vibratoire moyenne est E. Mais la répartition de cette énergie sur les N modes est fluctuante car les sources sont de nature aléatoire. Seule l'énergie moyenne E est supposée connue.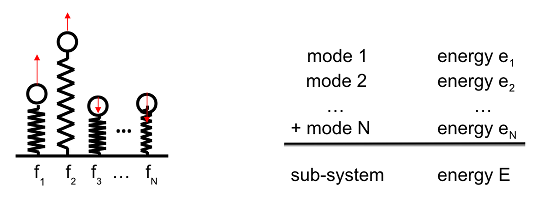
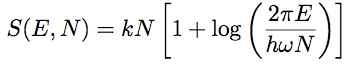 (6) (6)
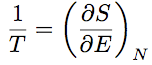
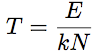 (7) (7)
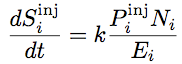
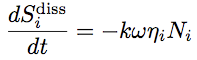
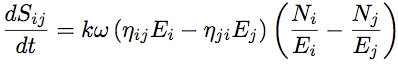
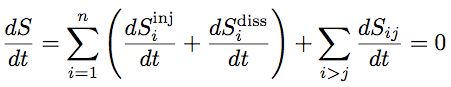

Echanges d’entropie vibroacoustique en SEA. Les sous-systèmes se comportent comme des réservoirs d'entropie. Chaque réservoir peut recevoir, dissiper et créer de l’entropie par mélange.Validité de la SEA.Quatre paramètres sont nécessaires pour qualifier le domaine de validité de la SEA [3, 5]
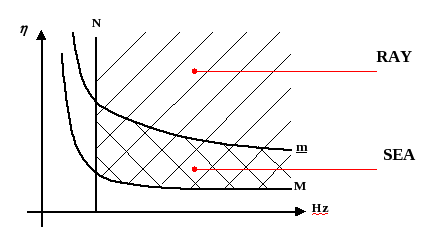
Domaine de validité de la SEA dans le cas d’un plaque en vibrations de flexion.Dans le plan fréquence – taux d’amortissement, ces quatre paramètres délimitent un domaine de validité pour la SEA. La ligne N=cte est une droite verticale, les lignes m=cte et M=cte sont des hyperboles. Le domaine de validité de la SEA est une bande étroite s’étendant jusqu’aux fréquences infinies. La méthode des rayons quant-à elle repose sur les deux conditions N>>1 et M>>1. Elle s’affranchit des deux autres conditions. Le domaine de validité des rayons est plus étendu que celui de la SEA. Une théorie récente.
Quelques applications.Tous les secteurs de l’industrie mécanique sont concernés, l’aéronautique, l’automobile, le train, l’électricité, le nucléaire, l’armement… La SEA est un outil puissant de pré-dimensionnement des structures et d’optimisation. Elle permet de connaître les flux d’énergie vibratoire et donc d’élaborer des stratégies de blocage de ces flux. Aujourd’hui très répandue dans l’industrie, la SEA a séduit les concepteurs plus en raison du regard différent qu’elle apporte sur les objets que pour la qualité de ses résultats prédictifs. Vers une thermodynamique hors équilibre…La difficulté principale de l’application de la SEA réside dans le trop faible nombre de degrés de liberté des systèmes usuels, de l’ordre de quelques centaines de modes à comparer avec le nombre d’Avogadro Bibliographie.[1] R.H. Lyon, Statistical Energy Analysis of Dynamical Systems: Theory and Application, Cambridge, Massachusetts, MIT Press, 1975. [2] R.H. Lyon and R.G. DeJong, Theory and Application of Statistical Energy Analysis, Boston, Butterworth-Heinemann, 1995. [3] A. Le Bot, Derivation of statistical energy analysis from radiative exchanges, Journal of Sound and Vibration, vol. 300, p. 763-779, 2007. [4] A. Le Bot, Entropy in statistical energy analysis, Journal of the Acoustical Society of America, vol. 125, p. 1473-1478 , 2009. [5] A. Le Bot and V. Cotoni, Validity diagrams of statistical energy analysis, Journal of Sound and Vibration, vol. 329, p. 221-235, 2010. |